High-energy inelastic scattering para-H2
- Hubert Jóźwiak
Input file
The input file can be found here.
Below, we provide the screenshot of this file.
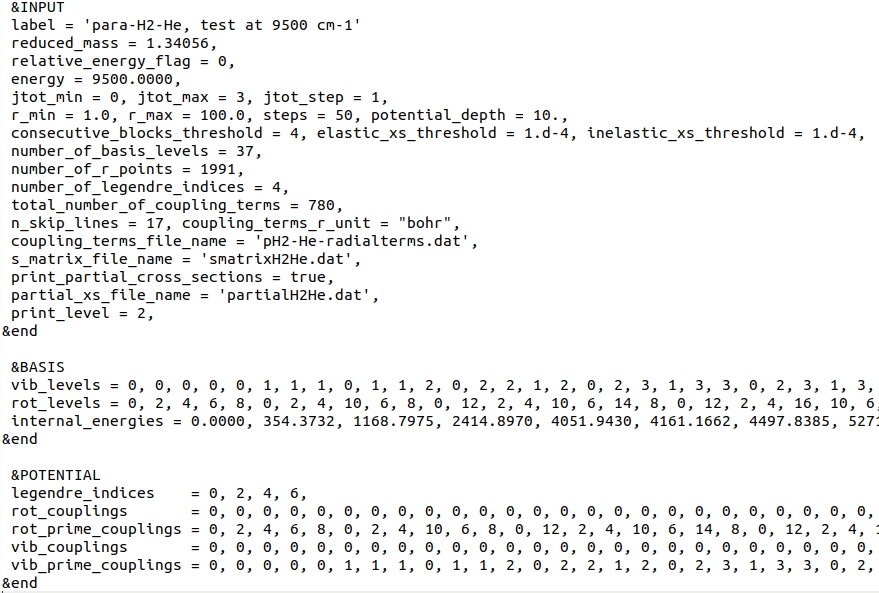
We choose to define collision energy through total energy by setting relative_energy_flag to 0: variable energy is thus interpreted as the total energy.
In this test, we fix the range of total angular momenta by setting jtot_min to 0 and jtot_max to 3.
This is because converged calculations (which should go up to \(J = 164\)) take too much time and the test just demonstrates capabilities of the code.
The basis in this test covers the same number of levels that were used in the calculations of H2-He rate coefficients in this paper:
number_of_basis_levels = 37.
This number is quite large and involves a lot of closed rovibrational levels at \(E_{\mathrm{tot}} =\) 9500 cm\(^{-1}\).
It was determined by performing convergence tests at the largest energy considered in calculatiions and kept fixed on the whole energy grid.
For details see Sec. 2 of this paper.
Vibrational and rotational quantum numbers, as well as corresponding internal energies of these levels are provided in the BASIS namelist, through vib_levels, rot_levels and internal_energies arrays.
Note that the screenshot does not cover all elements of internal_energies array.
The next 6 variables provide information about the radial coupling terms file, and where already discussed in the Elastic scattering test.
This time, however, the file is different (adjusted for para-H2-He coupling terms), and the total number of coupling terms is slightly smaller.
Namelist POTENTIAL provides the corresponding values of rovibrational quantum numbers describing each coupling term.
We keep the same name for S-matrix and partial state-to-state cross-sections files.
Output file
The output file can be found here.
Input parameters are summarized at the beginning of the file:
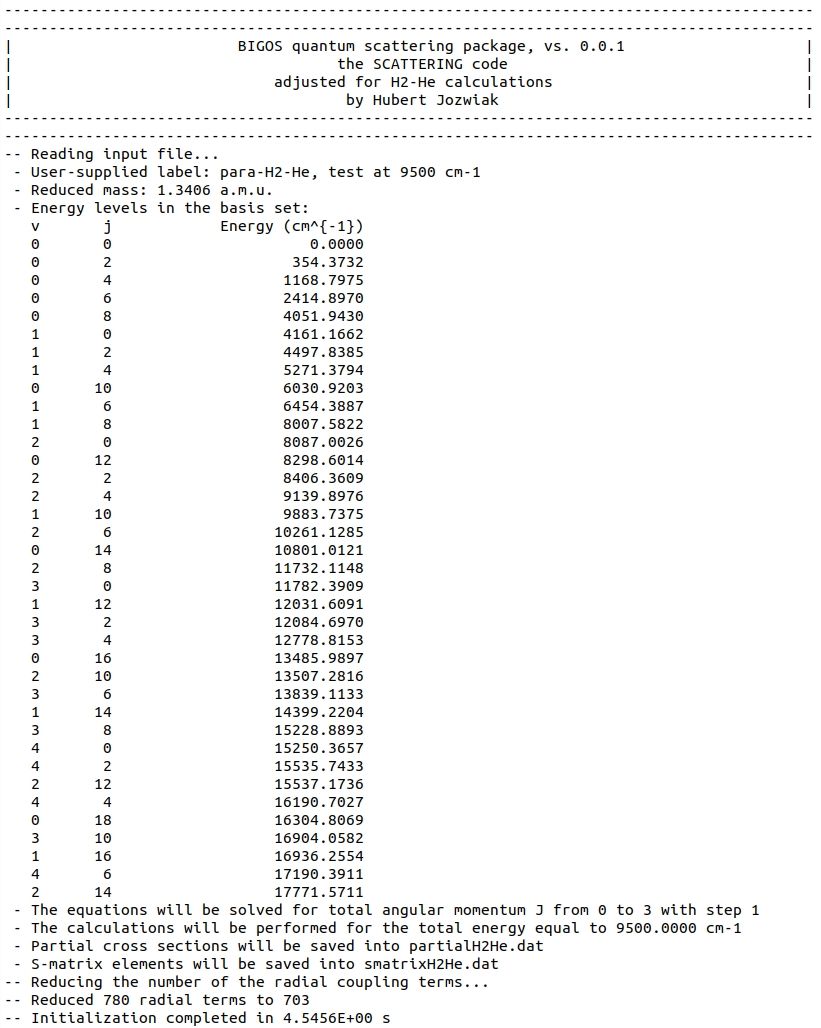
Note that out of the 780 coupling terms provided in the 'pH2-He-radialterms.dat' file, only 703 terms were actually used in the calculations (see reduce_radial_coupling_terms procedure).
This is because the basis involves 37 terms, and we need \( (37 \cdot 38) / 2 = 703\) unique radial terms to describe the \( (v,j) \leftrightarrow (v',j') \) couplings.
The information about each block is presented in the same way as in the Elastic scattering example.
Note that compared to the Inelastic scattering example for ortho-H2 which involved only 7 levels in the basis, the number of channels contributing to the, say \(J = 3, p = -1\) block is much higher:
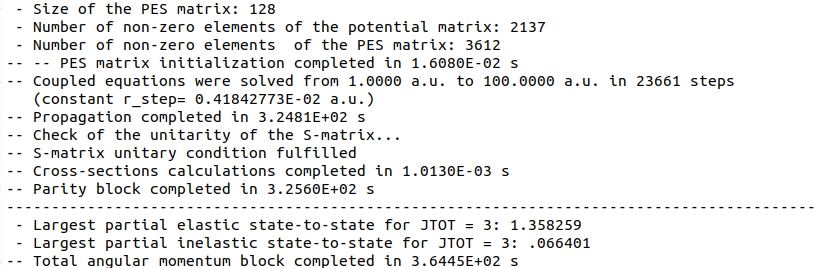
We have 128 channels, and in general, the coupling matrix should have \(128 \cdot 128 = 16 384\) elements.
However, only \( 2137 \) of them are non-zero, since the interaction potential does not couple \(\bar{\Omega}'\neq \bar{\Omega}\) blocks.
Using symmetry properties on 3-j symbols entering the formula for algebraic coefficients, \( g_{{\lambda},\gamma,\gamma'}^{Jp} \), one can show that only 3 612 coefficients are sufficient to describe the contribution from the PES to the Coupling Matrix.
At \(9500\) cm\(^{-1}\), there is already a quite large number of cross-sections that are energetically available.
The full list involves 224 cross-sections, and the following screenshots captures only the beginning of the list:
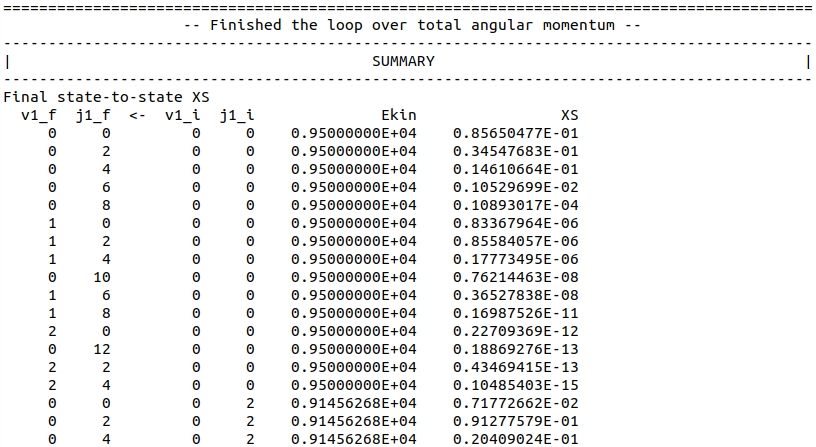
Please note that this test only demonstrates the capabilities of the code and does not provide fully converged cross-sections at \(E = 9500\) cm\(^{-1}\).
In order to obtain cross-sections converged to the level of \(10^{-4} Å^{2}\), calculations should be extended to \(J = 164\).
Other files
In addition to the output file, the calculations produce a file containing partial state-to-state cross-sections, which is available here, and the binary S-matrix file here. The latter one needs a post-processor to read and interpret the saved data.
Comparison with MOLSCAT
A correspodning MOLSCAT test is provided here:
- input.dat provides MOLSCAT's input file.
- output.dat is the output file from MOLSCAT calculations
Note that while BIGOS run took less than 700 seconds, the corresponding MOLSCAT run took 72055.98 seconds!
The results agree to the level better than 0.03%, as presented in the table below.
| \(v_{f}\) | \(j_{f}\) | \(v_{i}\) | \(j_{f}\) | \(E_{\mathrm{kin}}\) | BIGOS | MOLSCAT | Rel. Diff. (%) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 9500.00 | 8.5650E-02 | 8.5621E-02 | 0.034 |
| 0 | 2 | 0 | 0 | 9500.00 | 3.4548E-02 | 3.4548E-02 | 0.000 |
| 0 | 4 | 0 | 0 | 9500.00 | 1.4611E-02 | 1.4611E-02 | 0.000 |
| 0 | 6 | 0 | 0 | 9500.00 | 1.0530E-03 | 1.0530E-03 | 0.000 |
| 0 | 8 | 0 | 0 | 9500.00 | 1.0893E-05 | 1.0893E-05 | 0.001 |
| 1 | 0 | 0 | 0 | 9500.00 | 8.3368E-07 | 8.3368E-07 | 0.000 |
| 1 | 2 | 0 | 0 | 9500.00 | 8.5584E-07 | 8.5585E-07 | 0.001 |
| 1 | 4 | 0 | 0 | 9500.00 | 1.7773E-07 | 1.7774E-07 | 0.002 |
| 0 | 10 | 0 | 0 | 9500.00 | 7.6214E-09 | 7.6214E-09 | 0.001 |
| 1 | 6 | 0 | 0 | 9500.00 | 3.6528E-09 | 3.6528E-09 | 0.000 |
| 1 | 8 | 0 | 0 | 9500.00 | 1.6988E-12 | 1.6987E-12 | 0.000 |
| 2 | 0 | 0 | 0 | 9500.00 | 2.2709E-13 | 2.2709E-13 | 0.000 |
| 0 | 12 | 0 | 0 | 9500.00 | 1.8869E-14 | 1.8869E-14 | 0.000 |
| 2 | 2 | 0 | 0 | 9500.00 | 4.3469E-14 | 4.3469E-14 | 0.001 |
| 2 | 4 | 0 | 0 | 9500.00 | 1.0485E-16 | 1.0485E-16 | 0.002 |
| 0 | 0 | 0 | 2 | 9145.63 | 7.1773E-03 | 7.1773E-03 | 0.000 |
| 0 | 2 | 0 | 2 | 9145.63 | 9.1278E-02 | 9.1281E-02 | 0.004 |
| 0 | 4 | 0 | 2 | 9145.63 | 2.0409E-02 | 2.0409E-02 | 0.000 |
| 0 | 6 | 0 | 2 | 9145.63 | 2.6639E-03 | 2.6639E-03 | 0.000 |
| 0 | 8 | 0 | 2 | 9145.63 | 4.0431E-05 | 4.0430E-05 | 0.001 |
| 1 | 0 | 0 | 2 | 9145.63 | 1.2404E-07 | 1.2404E-07 | 0.000 |
| 1 | 2 | 0 | 2 | 9145.63 | 1.1180E-06 | 1.1180E-06 | 0.000 |
| 1 | 4 | 0 | 2 | 9145.63 | 3.6448E-07 | 3.6448E-07 | 0.000 |
| 0 | 10 | 0 | 2 | 9145.63 | 3.5867E-08 | 3.5866E-08 | 0.001 |
| 1 | 6 | 0 | 2 | 9145.63 | 1.0040E-08 | 1.0040E-08 | 0.000 |
| 1 | 8 | 0 | 2 | 9145.63 | 5.8557E-12 | 5.8556E-12 | 0.000 |
| 2 | 0 | 0 | 2 | 9145.63 | 1.6572E-13 | 1.6572E-13 | 0.001 |
| 0 | 12 | 0 | 2 | 9145.63 | 1.0300E-13 | 1.0300E-13 | 0.001 |
| 2 | 2 | 0 | 2 | 9145.63 | 7.0276E-14 | 7.0275E-14 | 0.001 |
| 2 | 4 | 0 | 2 | 9145.63 | 2.5855E-16 | 2.5855E-16 | 0.001 |
| 0 | 0 | 0 | 4 | 8331.20 | 1.8512E-03 | 1.8512E-03 | 0.000 |
| 0 | 2 | 0 | 4 | 8331.20 | 1.2447E-02 | 1.2447E-02 | 0.000 |
| 0 | 4 | 0 | 4 | 8331.20 | 6.3909E-02 | 6.3908E-02 | 0.002 |
| 0 | 6 | 0 | 4 | 8331.20 | 9.6658E-03 | 9.6657E-03 | 0.000 |
| 0 | 8 | 0 | 4 | 8331.20 | 2.9080E-04 | 2.9080E-04 | 0.001 |
| 1 | 0 | 0 | 4 | 8331.20 | 5.3028E-07 | 5.3028E-07 | 0.000 |
| 1 | 2 | 0 | 4 | 8331.20 | 2.7929E-06 | 2.7929E-06 | 0.000 |
| 1 | 4 | 0 | 4 | 8331.20 | 1.4826E-06 | 1.4826E-06 | 0.001 |
| 0 | 10 | 0 | 4 | 8331.20 | 3.8707E-07 | 3.8706E-07 | 0.001 |
| 1 | 6 | 0 | 4 | 8331.20 | 6.5708E-08 | 6.5708E-08 | 0.000 |
| 1 | 8 | 0 | 4 | 8331.20 | 5.4991E-11 | 5.4991E-11 | 0.001 |
| 2 | 0 | 0 | 4 | 8331.20 | 1.8206E-13 | 1.8206E-13 | 0.000 |
| 0 | 12 | 0 | 4 | 8331.20 | 1.4197E-12 | 1.4197E-12 | 0.000 |
| 2 | 2 | 0 | 4 | 8331.20 | 4.1636E-13 | 4.1635E-13 | 0.001 |
| 2 | 4 | 0 | 4 | 8331.20 | 1.8229E-15 | 1.8228E-15 | 0.001 |
| 0 | 0 | 0 | 6 | 7085.10 | 1.0861E-04 | 1.0860E-04 | 0.000 |
| 0 | 2 | 0 | 6 | 7085.10 | 1.3226E-03 | 1.3226E-03 | 0.001 |
| 0 | 4 | 0 | 6 | 7085.10 | 7.8686E-03 | 7.8686E-03 | 0.000 |
| 0 | 6 | 0 | 6 | 7085.10 | 5.9511E-02 | 5.9512E-02 | 0.001 |
| 0 | 8 | 0 | 6 | 7085.10 | 2.8382E-03 | 2.8382E-03 | 0.000 |
| 1 | 0 | 0 | 6 | 7085.10 | 4.5811E-07 | 4.5811E-07 | 0.000 |
| 1 | 2 | 0 | 6 | 7085.10 | 2.4600E-06 | 2.4600E-06 | 0.000 |
| 1 | 4 | 0 | 6 | 7085.10 | 6.2932E-06 | 6.2932E-06 | 0.000 |
| 0 | 10 | 0 | 6 | 7085.10 | 7.4249E-06 | 7.4249E-06 | 0.000 |
| 1 | 6 | 0 | 6 | 7085.10 | 7.4540E-07 | 7.4539E-07 | 0.000 |
| 1 | 8 | 0 | 6 | 7085.10 | 1.1122E-09 | 1.1122E-09 | 0.000 |
| 2 | 0 | 0 | 6 | 7085.10 | 1.4098E-12 | 1.4098E-12 | 0.000 |
| 0 | 12 | 0 | 6 | 7085.10 | 4.0187E-11 | 4.0187E-11 | 0.000 |
| 2 | 2 | 0 | 6 | 7085.10 | 3.2047E-12 | 3.2047E-12 | 0.000 |
| 2 | 4 | 0 | 6 | 7085.10 | 2.4531E-14 | 2.4531E-14 | 0.000 |
| 0 | 0 | 0 | 8 | 5448.06 | 1.1173E-06 | 1.1173E-06 | 0.001 |
| 0 | 2 | 0 | 8 | 5448.06 | 1.9962E-05 | 1.9962E-05 | 0.001 |
| 0 | 4 | 0 | 8 | 5448.06 | 2.3542E-04 | 2.3542E-04 | 0.001 |
| 0 | 6 | 0 | 8 | 5448.06 | 2.8226E-03 | 2.8226E-03 | 0.000 |
| 0 | 8 | 0 | 8 | 5448.06 | 6.6053E-02 | 6.6053E-02 | 0.001 |
| 1 | 0 | 0 | 8 | 5448.06 | 5.8392E-08 | 5.8392E-08 | 0.000 |
| 1 | 2 | 0 | 8 | 5448.06 | 5.1175E-07 | 5.1175E-07 | 0.000 |
| 1 | 4 | 0 | 8 | 5448.06 | 9.4312E-07 | 9.4312E-07 | 0.000 |
| 0 | 10 | 0 | 8 | 5448.06 | 3.1088E-04 | 3.1088E-04 | 0.000 |
| 1 | 6 | 0 | 8 | 5448.06 | 1.0331E-05 | 1.0331E-05 | 0.000 |
| 1 | 8 | 0 | 8 | 5448.06 | 5.3552E-08 | 5.3552E-08 | 0.000 |
| 2 | 0 | 0 | 8 | 5448.06 | 3.4358E-13 | 3.4358E-13 | 0.000 |
| 0 | 12 | 0 | 8 | 5448.06 | 3.2163E-09 | 3.2163E-09 | 0.000 |
| 2 | 2 | 0 | 8 | 5448.06 | 4.6122E-12 | 4.6122E-12 | 0.000 |
| 2 | 4 | 0 | 8 | 5448.06 | 5.1488E-13 | 5.1488E-13 | 0.000 |
| 0 | 0 | 1 | 0 | 5338.83 | 1.4835E-06 | 1.4835E-06 | 0.000 |
| 0 | 2 | 1 | 0 | 5338.83 | 1.0624E-06 | 1.0624E-06 | 0.000 |
| 0 | 4 | 1 | 0 | 5338.83 | 7.4474E-06 | 7.4474E-06 | 0.000 |
| 0 | 6 | 1 | 0 | 5338.83 | 7.9034E-06 | 7.9034E-06 | 0.000 |
| 0 | 8 | 1 | 0 | 5338.83 | 1.0130E-06 | 1.0130E-06 | 0.000 |
| 1 | 0 | 1 | 0 | 5338.83 | 1.3150E-01 | 1.3151E-01 | 0.008 |
| 1 | 2 | 1 | 0 | 5338.83 | 6.6148E-02 | 6.6148E-02 | 0.000 |
| 1 | 4 | 1 | 0 | 5338.83 | 1.6919E-02 | 1.6919E-02 | 0.000 |
| 0 | 10 | 1 | 0 | 5338.83 | 2.8303E-08 | 2.8303E-08 | 0.000 |
| 1 | 6 | 1 | 0 | 5338.83 | 3.7280E-04 | 3.7280E-04 | 0.000 |
| 1 | 8 | 1 | 0 | 5338.83 | 1.8357E-07 | 1.8357E-07 | 0.000 |
| 2 | 0 | 1 | 0 | 5338.83 | 3.7427E-08 | 3.7427E-08 | 0.000 |
| 0 | 12 | 1 | 0 | 5338.83 | 5.6868E-12 | 5.6868E-12 | 0.000 |
| 2 | 2 | 1 | 0 | 5338.83 | 8.5432E-09 | 8.5432E-09 | 0.000 |
| 2 | 4 | 1 | 0 | 5338.83 | 2.8831E-11 | 2.8831E-11 | 0.000 |
| 0 | 0 | 1 | 2 | 5002.16 | 3.2508E-07 | 3.2508E-07 | 0.001 |
| 0 | 2 | 1 | 2 | 5002.16 | 2.0440E-06 | 2.0440E-06 | 0.000 |
| 0 | 4 | 1 | 2 | 5002.16 | 8.3728E-06 | 8.3728E-06 | 0.000 |
| 0 | 6 | 1 | 2 | 5002.16 | 9.0595E-06 | 9.0595E-06 | 0.000 |
| 0 | 8 | 1 | 2 | 5002.16 | 1.8950E-06 | 1.8950E-06 | 0.000 |
| 1 | 0 | 1 | 2 | 5002.16 | 1.4120E-02 | 1.4120E-02 | 0.000 |
| 1 | 2 | 1 | 2 | 5002.16 | 1.7367E-01 | 1.7367E-01 | 0.001 |
| 1 | 4 | 1 | 2 | 5002.16 | 2.9273E-02 | 2.9273E-02 | 0.000 |
| 0 | 10 | 1 | 2 | 5002.16 | 9.3847E-08 | 9.3847E-08 | 0.000 |
| 1 | 6 | 1 | 2 | 5002.16 | 1.1262E-03 | 1.1262E-03 | 0.000 |
| 1 | 8 | 1 | 2 | 5002.16 | 7.8991E-07 | 7.8991E-07 | 0.000 |
| 2 | 0 | 1 | 2 | 5002.16 | 1.8360E-08 | 1.8360E-08 | 0.000 |
| 0 | 12 | 1 | 2 | 5002.16 | 2.6463E-11 | 2.6463E-11 | 0.000 |
| 2 | 2 | 1 | 2 | 5002.16 | 1.6756E-08 | 1.6756E-08 | 0.000 |
| 2 | 4 | 1 | 2 | 5002.16 | 8.5546E-11 | 8.5545E-11 | 0.000 |
| 0 | 0 | 1 | 4 | 4228.62 | 4.4367E-08 | 4.4367E-08 | 0.001 |
| 0 | 2 | 1 | 4 | 4228.62 | 4.3794E-07 | 4.3794E-07 | 0.000 |
| 0 | 4 | 1 | 4 | 4228.62 | 2.9210E-06 | 2.9210E-06 | 0.001 |
| 0 | 6 | 1 | 4 | 4228.62 | 1.5231E-05 | 1.5231E-05 | 0.000 |
| 0 | 8 | 1 | 4 | 4228.62 | 2.2952E-06 | 2.2952E-06 | 0.000 |
| 1 | 0 | 1 | 4 | 4228.62 | 2.3735E-03 | 2.3735E-03 | 0.000 |
| 1 | 2 | 1 | 4 | 4228.62 | 1.9238E-02 | 1.9238E-02 | 0.000 |
| 1 | 4 | 1 | 4 | 4228.62 | 1.4673E-01 | 1.4673E-01 | 0.000 |
| 0 | 10 | 1 | 4 | 4228.62 | 6.6590E-07 | 6.6590E-07 | 0.000 |
| 1 | 6 | 1 | 4 | 4228.62 | 7.2620E-03 | 7.2619E-03 | 0.000 |
| 1 | 8 | 1 | 4 | 4228.62 | 9.5330E-06 | 9.5329E-06 | 0.000 |
| 2 | 0 | 1 | 4 | 4228.62 | 3.5020E-08 | 3.5020E-08 | 0.000 |
| 0 | 12 | 1 | 4 | 4228.62 | 3.5580E-10 | 3.5580E-10 | 0.000 |
| 2 | 2 | 1 | 4 | 4228.62 | 1.0123E-07 | 1.0123E-07 | 0.000 |
| 2 | 4 | 1 | 4 | 4228.62 | 7.0689E-10 | 7.0689E-10 | 0.000 |
| 0 | 0 | 0 | 10 | 3469.08 | 9.9387E-10 | 9.9386E-10 | 0.001 |
| 0 | 2 | 0 | 10 | 3469.08 | 2.2513E-08 | 2.2513E-08 | 0.001 |
| 0 | 4 | 0 | 10 | 3469.08 | 3.9838E-07 | 3.9838E-07 | 0.001 |
| 0 | 6 | 0 | 10 | 3469.08 | 9.3874E-06 | 9.3874E-06 | 0.000 |
| 0 | 8 | 0 | 10 | 3469.08 | 3.9523E-04 | 3.9523E-04 | 0.000 |
| 1 | 0 | 0 | 10 | 3469.08 | 2.0742E-09 | 2.0742E-09 | 0.000 |
| 1 | 2 | 0 | 10 | 3469.08 | 3.2219E-08 | 3.2219E-08 | 0.000 |
| 1 | 4 | 0 | 10 | 3469.08 | 3.4787E-07 | 3.4787E-07 | 0.000 |
| 0 | 10 | 0 | 10 | 3469.08 | 9.2517E-02 | 9.2518E-02 | 0.001 |
| 1 | 6 | 0 | 10 | 3469.08 | 8.3263E-06 | 8.3263E-06 | 0.000 |
| 1 | 8 | 0 | 10 | 3469.08 | 8.9217E-06 | 8.9217E-06 | 0.000 |
| 2 | 0 | 0 | 10 | 3469.08 | 4.7321E-13 | 4.7321E-13 | 0.000 |
| 0 | 12 | 0 | 10 | 3469.08 | 1.6117E-06 | 1.6117E-06 | 0.000 |
| 2 | 2 | 0 | 10 | 3469.08 | 1.7422E-11 | 1.7422E-11 | 0.000 |
| 2 | 4 | 0 | 10 | 3469.08 | 1.0705E-11 | 1.0705E-11 | 0.000 |
| 0 | 0 | 1 | 6 | 3045.61 | 8.7645E-10 | 8.7646E-10 | 0.000 |
| 0 | 2 | 1 | 6 | 3045.61 | 1.1596E-08 | 1.1596E-08 | 0.000 |
| 0 | 4 | 1 | 6 | 3045.61 | 1.2444E-07 | 1.2444E-07 | 0.000 |
| 0 | 6 | 1 | 6 | 3045.61 | 1.7340E-06 | 1.7340E-06 | 0.000 |
| 0 | 8 | 1 | 6 | 3045.61 | 2.4166E-05 | 2.4166E-05 | 0.000 |
| 1 | 0 | 1 | 6 | 3045.61 | 5.0270E-05 | 5.0270E-05 | 0.000 |
| 1 | 2 | 1 | 6 | 3045.61 | 7.1141E-04 | 7.1141E-04 | 0.000 |
| 1 | 4 | 1 | 6 | 3045.61 | 6.9803E-03 | 6.9803E-03 | 0.000 |
| 0 | 10 | 1 | 6 | 3045.61 | 1.5320E-05 | 1.5320E-05 | 0.000 |
| 1 | 6 | 1 | 6 | 3045.61 | 1.5784E-01 | 1.5784E-01 | 0.000 |
| 1 | 8 | 1 | 6 | 3045.61 | 3.4166E-04 | 3.4166E-04 | 0.000 |
| 2 | 0 | 1 | 6 | 3045.61 | 2.0933E-08 | 2.0933E-08 | 0.000 |
| 0 | 12 | 1 | 6 | 3045.61 | 1.5931E-08 | 1.5931E-08 | 0.000 |
| 2 | 2 | 1 | 6 | 3045.61 | 5.7683E-08 | 5.7683E-08 | 0.000 |
| 2 | 4 | 1 | 6 | 3045.61 | 1.0461E-08 | 1.0461E-08 | 0.000 |
| 0 | 0 | 1 | 8 | 1492.42 | 6.3608E-13 | 6.3608E-13 | 0.000 |
| 0 | 2 | 1 | 8 | 1492.42 | 1.0554E-11 | 1.0554E-11 | 0.001 |
| 0 | 4 | 1 | 8 | 1492.42 | 1.6252E-10 | 1.6252E-10 | 0.000 |
| 0 | 6 | 1 | 8 | 1492.42 | 4.0376E-09 | 4.0376E-09 | 0.000 |
| 0 | 8 | 1 | 8 | 1492.42 | 1.9549E-07 | 1.9549E-07 | 0.000 |
| 1 | 0 | 1 | 8 | 1492.42 | 3.8629E-08 | 3.8629E-08 | 0.000 |
| 1 | 2 | 1 | 8 | 1492.42 | 7.7870E-07 | 7.7869E-07 | 0.000 |
| 1 | 4 | 1 | 8 | 1492.42 | 1.4300E-05 | 1.4300E-05 | 0.000 |
| 0 | 10 | 1 | 8 | 1492.42 | 2.5618E-05 | 2.5618E-05 | 0.000 |
| 1 | 6 | 1 | 8 | 1492.42 | 5.3318E-04 | 5.3318E-04 | 0.000 |
| 1 | 8 | 1 | 8 | 1492.42 | 2.4658E-01 | 2.4658E-01 | 0.000 |
| 2 | 0 | 1 | 8 | 1492.42 | 6.3769E-09 | 6.3769E-09 | 0.000 |
| 0 | 12 | 1 | 8 | 1492.42 | 1.7897E-05 | 1.7897E-05 | 0.000 |
| 2 | 2 | 1 | 8 | 1492.42 | 1.2744E-07 | 1.2744E-07 | 0.000 |
| 2 | 4 | 1 | 8 | 1492.42 | 2.4081E-07 | 2.4081E-07 | 0.000 |
| 0 | 0 | 2 | 0 | 1413.00 | 1.5268E-12 | 1.5268E-12 | 0.000 |
| 0 | 2 | 2 | 0 | 1413.00 | 5.3632E-12 | 5.3632E-12 | 0.001 |
| 0 | 4 | 2 | 0 | 1413.00 | 9.6612E-12 | 9.6612E-12 | 0.000 |
| 0 | 6 | 2 | 0 | 1413.00 | 9.1899E-11 | 9.1898E-11 | 0.000 |
| 0 | 8 | 2 | 0 | 1413.00 | 2.2520E-11 | 2.2520E-11 | 0.000 |
| 1 | 0 | 2 | 0 | 1413.00 | 1.4141E-07 | 1.4141E-07 | 0.000 |
| 1 | 2 | 2 | 0 | 1413.00 | 3.2498E-07 | 3.2498E-07 | 0.000 |
| 1 | 4 | 2 | 0 | 1413.00 | 9.4324E-07 | 9.4324E-07 | 0.000 |
| 0 | 10 | 2 | 0 | 1413.00 | 2.4398E-11 | 2.4398E-11 | 0.000 |
| 1 | 6 | 2 | 0 | 1413.00 | 5.8656E-07 | 5.8656E-07 | 0.000 |
| 1 | 8 | 2 | 0 | 1413.00 | 1.1450E-07 | 1.1450E-07 | 0.000 |
| 2 | 0 | 2 | 0 | 1413.00 | 9.1930E-01 | 9.1930E-01 | 0.000 |
| 0 | 12 | 2 | 0 | 1413.00 | 4.5507E-12 | 4.5508E-12 | 0.000 |
| 2 | 2 | 2 | 0 | 1413.00 | 1.5319E-01 | 1.5319E-01 | 0.000 |
| 2 | 4 | 2 | 0 | 1413.00 | 7.1004E-04 | 7.1004E-04 | 0.000 |
| 0 | 0 | 0 | 12 | 1201.40 | 5.9683E-15 | 5.9683E-15 | 0.000 |
| 0 | 2 | 0 | 12 | 1201.40 | 1.5682E-13 | 1.5682E-13 | 0.001 |
| 0 | 4 | 0 | 12 | 1201.40 | 3.5442E-12 | 3.5442E-12 | 0.000 |
| 0 | 6 | 0 | 12 | 1201.40 | 1.2324E-10 | 1.2324E-10 | 0.000 |
| 0 | 8 | 0 | 12 | 1201.40 | 9.9180E-09 | 9.9180E-09 | 0.000 |
| 1 | 0 | 0 | 12 | 1201.40 | 1.0109E-12 | 1.0109E-12 | 0.000 |
| 1 | 2 | 0 | 12 | 1201.40 | 2.2036E-11 | 2.2036E-11 | 0.000 |
| 1 | 4 | 0 | 12 | 1201.40 | 4.5084E-10 | 4.5084E-10 | 0.000 |
| 0 | 10 | 0 | 12 | 1201.40 | 3.9092E-06 | 3.9092E-06 | 0.000 |
| 1 | 6 | 0 | 12 | 1201.40 | 2.1001E-08 | 2.1001E-08 | 0.000 |
| 1 | 8 | 0 | 12 | 1201.40 | 1.5118E-05 | 1.5118E-05 | 0.000 |
| 2 | 0 | 0 | 12 | 1201.40 | 2.1409E-13 | 2.1409E-13 | 0.000 |
| 0 | 12 | 0 | 12 | 1201.40 | 2.3663E-01 | 2.3663E-01 | 0.000 |
| 2 | 2 | 0 | 12 | 1201.40 | 3.6403E-12 | 3.6403E-12 | 0.000 |
| 2 | 4 | 0 | 12 | 1201.40 | 6.6529E-11 | 6.6529E-11 | 0.000 |
| 0 | 0 | 2 | 2 | 1093.64 | 7.5520E-14 | 7.5519E-14 | 0.001 |
| 0 | 2 | 2 | 2 | 1093.64 | 5.8769E-13 | 5.8768E-13 | 0.001 |
| 0 | 4 | 2 | 2 | 1093.64 | 5.7092E-12 | 5.7091E-12 | 0.001 |
| 0 | 6 | 2 | 2 | 1093.64 | 5.3980E-11 | 5.3980E-11 | 0.000 |
| 0 | 8 | 2 | 2 | 1093.64 | 7.8119E-11 | 7.8119E-11 | 0.000 |
| 1 | 0 | 2 | 2 | 1093.64 | 8.3411E-09 | 8.3411E-09 | 0.000 |
| 1 | 2 | 2 | 2 | 1093.64 | 7.6641E-08 | 7.6640E-08 | 0.000 |
| 1 | 4 | 2 | 2 | 1093.64 | 7.0452E-07 | 7.0452E-07 | 0.000 |
| 0 | 10 | 2 | 2 | 1093.64 | 2.3211E-10 | 2.3211E-10 | 0.000 |
| 1 | 6 | 2 | 2 | 1093.64 | 4.1766E-07 | 4.1766E-07 | 0.000 |
| 1 | 8 | 2 | 2 | 1093.64 | 5.9127E-07 | 5.9127E-07 | 0.000 |
| 2 | 0 | 2 | 2 | 1093.64 | 3.9586E-02 | 3.9586E-02 | 0.000 |
| 0 | 12 | 2 | 2 | 1093.64 | 1.9995E-11 | 1.9995E-11 | 0.000 |
| 2 | 2 | 2 | 2 | 1093.64 | 9.5964E-01 | 9.5964E-01 | 0.000 |
| 2 | 4 | 2 | 2 | 1093.64 | 4.2510E-03 | 4.2510E-03 | 0.000 |
| 0 | 0 | 2 | 4 | 360.10 | 3.0735E-16 | 3.0735E-16 | 0.002 |
| 0 | 2 | 2 | 4 | 360.10 | 3.6481E-15 | 3.6481E-15 | 0.001 |
| 0 | 4 | 2 | 4 | 360.10 | 4.2173E-14 | 4.2173E-14 | 0.001 |
| 0 | 6 | 2 | 4 | 360.10 | 6.9717E-13 | 6.9717E-13 | 0.000 |
| 0 | 8 | 2 | 4 | 360.10 | 1.4714E-11 | 1.4714E-11 | 0.000 |
| 1 | 0 | 2 | 4 | 360.10 | 4.7495E-11 | 4.7495E-11 | 0.000 |
| 1 | 2 | 2 | 4 | 360.10 | 6.6017E-10 | 6.6017E-10 | 0.000 |
| 1 | 4 | 2 | 4 | 360.10 | 8.3009E-09 | 8.3009E-09 | 0.000 |
| 0 | 10 | 2 | 4 | 360.10 | 2.4063E-10 | 2.4063E-10 | 0.000 |
| 1 | 6 | 2 | 4 | 360.10 | 1.2780E-07 | 1.2780E-07 | 0.000 |
| 1 | 8 | 2 | 4 | 360.10 | 1.8852E-06 | 1.8852E-06 | 0.000 |
| 2 | 0 | 2 | 4 | 360.10 | 3.0957E-04 | 3.0957E-04 | 0.000 |
| 0 | 12 | 2 | 4 | 360.10 | 6.1656E-10 | 6.1656E-10 | 0.000 |
| 2 | 2 | 2 | 4 | 360.10 | 7.1725E-03 | 7.1725E-03 | 0.000 |
| 2 | 4 | 2 | 4 | 360.10 | 2.1761E+00 | 2.1761E+00 | 0.000 |